[ML] MAE(Mean Absolute Error, 평균 절대 오차)

 MAE는 이전 포스팅의 MSE를 구하는 방법과 매우 유사하지만 가져오는 결과는 매우 다르다. MAE 역시 모델을 통한 예측값과 실제값의 차이를 바탕으로 평균을 구하지만, MSE와 다른 점은 제곱을 하지 않는 것이다. 따라서 MAE는 이상점(outlier)의 비중이 MSE에 비해 현저히 적다. 하지만 절대값을 다루기에 MSE와 마찬가지로 양수를 다루기에 예측값이 실제값보다 큰 값인지 작은 값인지에 대한 판단이 불가하다.

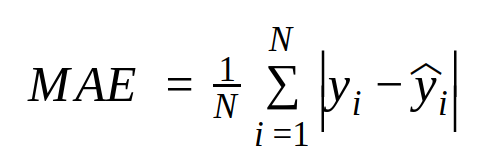
import numpy as np
import matplotlib.pyplot as plt

# MAE loss function
def mae_loss(y_pred, y_true):
    abs_error = np.abs(y_pred - y_true)
    sum_abs_error = np.sum(abs_error)
    loss = sum_abs_error / y_true.size
    return loss
    
# Plotting
x_vals = np.arange(-100, 100, 0.01)
y_vals = np.abs(x_vals)

plt.plot(x_vals, y_vals, "red")
plt.grid(True, which="major")
plt.show()

 

출처

- https://www.ibm.com/docs/en/cloud-paks/cp-data/3.0.1?topic=overview-mean-absolute-error 

- https://towardsdatascience.com/understanding-the-3-most-common-loss-functions-for-machine-learning-regression-23e0ef3e14d3